基础总结-数据结构
[toc]
排序
冒泡排序
原理:
两两比较相邻记录的关键字,如果反序则交换。时间复杂度最好情况下: o(n),最坏是(n*n)
//冒泡排序 相邻两个元素比较 时间复杂度:最坏是O(n^2) 最好的情况下O(n)
void BubbleSort(int* a, int len)
{
for (int i = 0; i < len; ++i)
{
bool noswap = true;
for (int j = 0; j < len - i - 1; ++j)
{
if (a[j] > a[j + 1])
{
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
noswap = false;
}
}
if (noswap)
{
break;
}
}
}
直接插入排序
原理:
直接插入排序算法 基本操作是将一个记录插入到已经排好序的有序表中,从而等到一个新的,元素加1的有序表 知道结束;
时间复杂度:最坏是O(n^2) 最好的情况下O(n)
void InsertSort(int* a, int len)
{
int idx = 0;
int temp = 0;
for (int i = 1; i < len; ++i)
{
temp = a[i];
for (idx = i - 1; idx >= 0 && a[idx] > temp; --idx)
{
a[idx + 1] = a[idx];
}
a[idx + 1] = temp;
}
}
选择排序
原理:
每次从乱序数组中找到最大(最小)的值,放在当前乱序数组头部,最终使数组有序; 时间复杂度:平均为O(n^2);最坏为:O(n^2)
void SelectSort(int* a, int len)
{
for (int i = 0; i < len; ++i)
{
int min = i;
for (int j = i + 1; j < len; ++j)
{
if (a[j] < a[min])
{
min = j;
}
}
if (i != min)
{
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}
快速排序
选择一个基准数,把比这个数小的挪到左边 这个数大的移动到右边 然后不断对左右两边执行这个操作 直到数组有序; 时间复杂度:平均时间复杂度:O(nlog2n); 最坏是:O(n^2);
//快速排序 选择一个基准数,把比这个数小的挪到左边 这个数大的移动到右边 然后不断对左右两边执行这个操作 直到数组有序
//时间复杂度:平均时间复杂度:O(nlog2n);
int Partition(int* nums, int low, int high);
void QuickSort(int* nums, int begin, int end)
{
if (begin < end)
{
int key = Partition(nums, begin, end);
if (key - 1 > 0)
{
QuickSort(nums, begin, key - 1);
}
if (key + 1 < end)
{
QuickSort(nums, key + 1, end);
}
}
}
/*
* 第一趟快速排序
*/
int Partition(int* nums, int low, int high)
{
if (nums == nullptr || low >= high)
{
//input invaild
return -1;
}
int guard = nums[low];
while (low < high)
{
while (low < high && nums[high] >= guard)
{
--high;
}
if (low < high)
{
nums[low] = nums[high];
++low;
}
while (low < high && nums[low] < guard)
{
++low;
}
if (low < high)
{
nums[high] = nums[low];
--high;
}
}
nums[low] = guard;
return low;
}
希尔(shell)排序
原理: 希尔排序:又叫缩小增量排序方法;是一种基于插入思想的排序方法; 通过逐一减少增量的方法,使得一个数组逐渐达到有序的目的;以上就是希尔排序的思路了,总的来说,就是每次选定一个步长,将数组进行划分,然后对每列小划分利用直接插入排序方法排序,得到新数组,再选择步长分组,利用直接插入排序。直到步长为1,最后利用一次直接插入排序。说白了,希尔排序就是选择合适步长+直接插入排序。
时间复杂度:平均是O(n^1.3),最好:O(n) 最坏:O(n^2)
//shell排序 希尔排序是将数组按照一定步长分成几个子数组进行排序,通过逐渐缩短步长来完成最终排序
//时间复杂度:O(nlogn) ~~ O(n^2);
void ShellSort(int* a, int len)
{
for (int gap = len >> 1; gap > 0; gap >>= 1)
{
for (int i = gap; i < len; ++i)
{
int temp = a[i];
int j = i - gap;
for (; j >= 0 && a[j] > temp; j -= gap)
{
a[j + gap] = a[j];
}
a[j + gap] = temp;
}
}
}
归并排序
归并排序的基本思想是将若干个序列进行两两归并,直至所有待排序记录都在一个有序序列为止;
时间复杂度: 平均时间复杂度: O(nlog2n); 最好最坏都是: O(nlog2n);
//归并排序 将一个数组打散成小数组,然后把小数组拼凑再排序知道数组有序
void MergeArray(int* nums, int begin, int mid, int end, int* temp)
{
int low = begin;
int high = mid;
int temp_idx = begin;
while (low != mid && high != end)
{
if (nums[low] < nums[high])
{
temp[temp_idx++] = nums[low++];
}
else
{
temp[temp_idx++] = nums[high++];
}
}
while (low < mid)
{
temp[temp_idx++] = nums[low++];
}
while (high < end)
{
temp[temp_idx++] = nums[high++];
}
}
void MergeSort(int* nums, int begin, int end, int* temp)
{
int mid = (begin + end) / 2;
if (mid != begin)
{
MergeSort(nums, begin, mid, temp);
MergeSort(nums, mid, end, temp);
MergeArray(nums, begin, mid, end, temp);
}
}
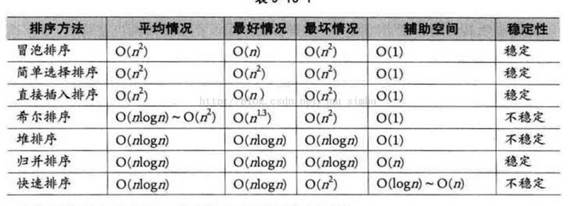
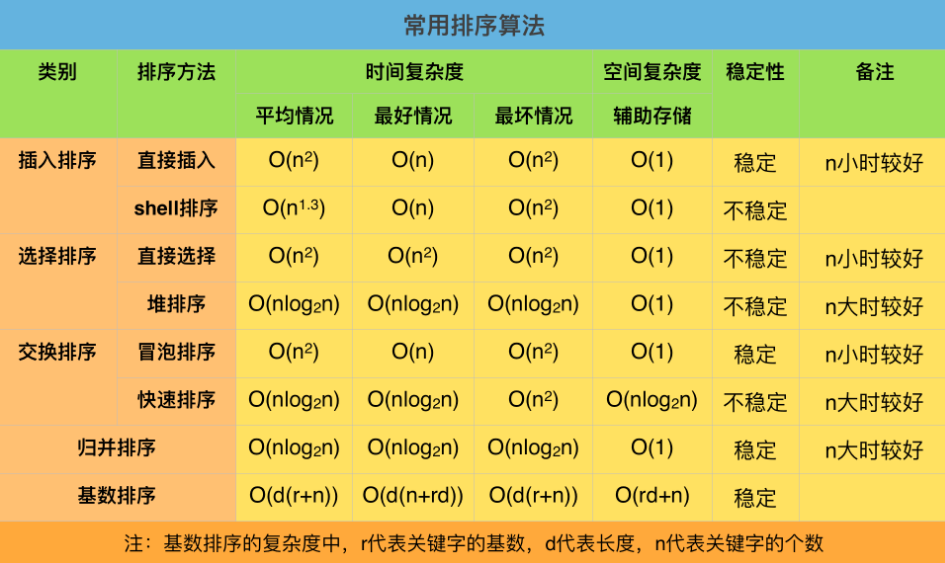
排序算法时间复杂度
堆
堆(Heap)分为小根堆和大根堆两种;
对于一个小根堆,它是具有如下特性的一棵完全二叉树:
- 若树根结点存在左孩子,则根结点的值(或某个域的值)小于等于左孩子结点的值(或某个域的值);
- 若树根结点存在右孩子,则根结点的值(或某个域的值)小于等于右孩子结点的值(或某个域的值);
- 以左、右孩子为根的子树又各是一个堆。
大根堆的定义与上述类似,只要把小于等于改为大于等于就得到了。
重建堆
当堆顶改变时候,如何重建堆??
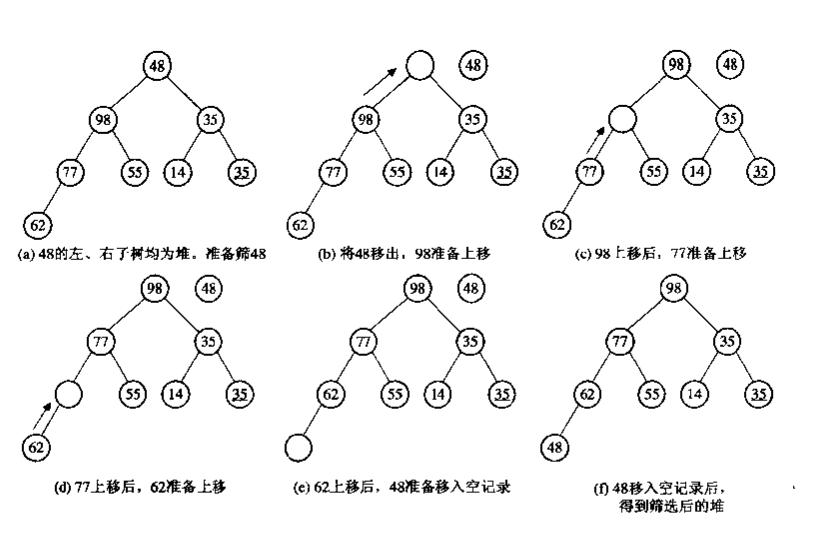
/*
* 调整堆
* 参数:heap[begin, end]是以heap[begin]为根的完全二叉树;
* 且分别以heap[2*begin] 和 [2*begin + 1]为根的左右子树为大根堆;
* 调整heap[begin]使其符合大根堆;
*/
void AdjustHeap(int* heap, int begin, int end)
{
if (heap == nullptr || begin >= end)
{
return;
}
int root_value = heap[begin];
int root = begin;
int child = root * 2;
bool finish = false;
while (child <= end && !finish)
{
if (child < end && heap[child] < heap[child + 1])
{
++child;
}
if (root_value >= heap[child])
{
finish = true;
}
else
{
heap[root] = heap[child];
root = child;
child = root * 2;
}
}
heap[root] = root_value;
}
如何由一任意序列出建堆
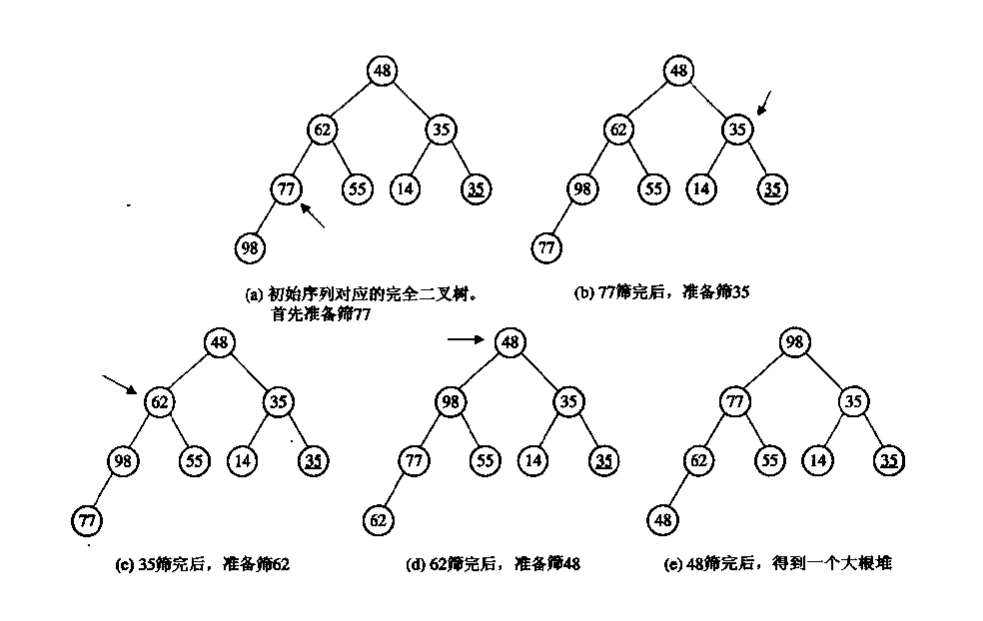
void CreateHeap(int* heap, int length)
{
if (heap == nullptr || length == 0)
{
return;
}
//从length / 2个记录开始进行筛选建堆
for (int index = length / 2; index >= 0; --index)
{
AdjustHeap(heap, index, length - 1);
}
}
堆排序
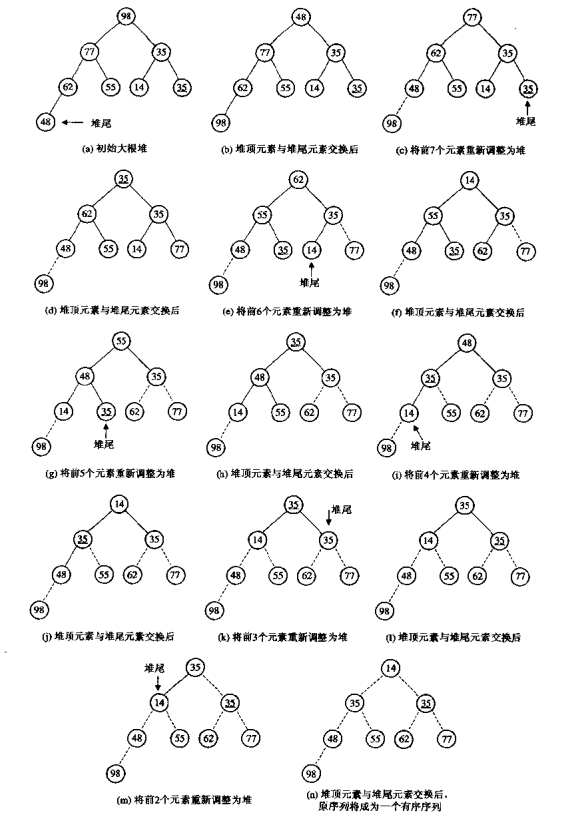
/*
* 堆排序 时间复杂度: 平均最好最坏都是O(log2n)
*/
void SortHeap(int* heap, int length)
{
int mid = length / 2;
for (int index = length - 1; index >= 1; --index)
{
//根节点和尾节点交换
int temp = heap[0];
heap[0] = heap[index];
heap[index] = temp;
AdjustHeap(heap, 0, index - 1);
}
}
查找算法
顺序查找
顺序查找算法 无序查找,属于线性查找 从序列到一端开始一次遍历; 时间复杂度:O(n)
int SequenceSearch(int arr[], int length, int value)
{
int index = 0;
for (int idx = 0; idx < length; ++idx)
{
if (arr[idx] == value)
{
return idx;
}
}
return -1;
}
二分查找
二分查找也叫折半查找;
- 思想:根据给定的值和序列的值对比,相等 找到;不等 再依次查找左右子序列;
- 注意:1. 二分查找的序列必须为有序序列,如果是无序的话,先排序; 2. 对于插入删除频繁的队列,维护有序队列成本较高,不建议使用;
- 时间复杂度:最坏是:O(log2(n + 1)); 平均:O(log2n)
int BinarySearch(int arr[], int length, int value)
{
int mid = 0;
int low = 0;
int high = length - 1;
while (low < high)
{
mid = (low + high) / 2;
if (arr[mid] == value)
{
return mid;
}
else if (arr[mid] < value)
{
low = mid + 1;
}
else
{
high = mid - 1;
}
}
return -1;
}
//迭代查找
int BinarySearchRe(int arr[], int low, int high, int value)
{
if (low < high)
{
return -1;
}
int mid = (low + high) / 2;
if (arr[mid] == value)
{
return mid;
}
else if (arr[mid] < value)
{
return BinarySearchRe(arr, mid + 1, high, value);
}
else
{
return BinarySearchRe(arr, low, mid - 1, value);
}
}
插值查找算法
- 思想:基于二分查找算法,根据查找点在序列中的大概位置,将查找点修改为自适应的,提高查找效率;
- 注: 对于表长较大,而且元素分布比较均匀的表来说,该算法平均性能比二分查找要好很多,反之,不一定合适
- 时间复杂度:查找成功或者失败的时间复杂度均为O(log2(log2n))
-
int InsertionSearch(int arr[], int length, int value) { int mid = 0; int low = 0; int high = length - 1; while (low < high) { mid = low + (value - arr[low]) / (arr[high] - arr[low])*(high - low); if (arr[mid] == value) { return mid; } else if (arr[mid] < value) { low = mid + 1; } else { high = mid - 1; } } return -1; }
树
树的类型
二叉排序树
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
- 二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
二叉排序树创建,插入,查找
二叉排序树的查找效率:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。查找长度: n(当为单支树), 平均长度:n(n+1)/2;
/*
* 关于二叉排序树的插入、生成、查找
*/
/*
* 根据二叉排序树的性质,二叉排序树插入
*/
typedef BinaryTreeNode BSTree;
void InsertBST(BSTree** tree, int key)
{
//二叉排序树插入遇到tree的value和key相等 直接退出
BSTree* bstree = nullptr;
if (*tree == nullptr)
{
bstree = new BinaryTreeNode();
bstree->value = key;
bstree->left = nullptr;
bstree->right = nullptr;
*tree = bstree;
}
else if ((*tree)->value < key)
{
InsertBST(&((*tree)->right), key);
}
else if ((*tree)->value > key)
{
InsertBST(&((*tree)->left), key);
}
}
/*
* 创建二叉排序树
*/
void CreateBST(int* tree, int length)
{
BSTree* bt = nullptr;
BSTree** bstree = &bt;
for (int index = 0; index < length; ++index)
{
InsertBST(bstree, tree[index]);
}
}
/*
* 二叉排序树 查找 递归
*/
BSTree* SearchBSTRe(BSTree* tree, int key)
{
if (tree == nullptr)
{
return nullptr;
}
else if (tree->value < key)
{
return SearchBSTRe(tree->right, key);
}
else
{
return SearchBSTRe(tree->left, key);
}
}
/*
* Binary Sort Tree search not recursion
*/
BSTree* SearchBST(BSTree* tree, int key)
{
BSTree* temp = tree;
while (temp)
{
if (temp->value == key)
{
return temp;
}
else if (temp->value < key)
{
temp = temp->right;
}
else
{
temp = temp->left;
}
}
}
平衡二叉排序树
平衡二叉排序树又称为AV树;一课平衡二叉树或者是空树,或者具有以下性质:
- 左子树和右子树的深度差绝对值小于等于1;
- 左右子树也是平衡二叉排序树;
平衡二叉排序树引入的目的:为了提高查找效率,其平均查找长度为O(log2n);
hash
哈希法又称散列法,我们使用一个下标范围比较大的数组来存储元素。可以设计一个函数(哈希函数, 也叫做散列函数),使得每个元素的关键字都与一个函数值(即数组下标)相对应,于是用这个数组单元来存储这个元素;也可以简单的理解为,按照关键字为每一个元素”分类”,然后将这个元素存储在相应”类”所对应的地方。但是,不能够保证每个元素的关键字与函数值是一一对应的,因此极有可能出现对于不同的元素,却计算出了相同的函数值,这样就产生了”冲突”;
什么是哈希函数?
哈希函数的规则是:通过某种转换关系,使关键字适度的分散到指定大小的的顺序结构中,越分散,则以后查找的时间复杂度越小,空间复杂度越高。
哈希函数本身便于计算;计算出来的结构分布均匀,尽可能的减少冲突;
哈希函数构造方式
数据分析法;
预先知道所有的数据,分析数据非分布,找出相应的方式;
平方取中法;
分段叠加法;
除留余数法;
伪随机法;
处理冲突的方法
开放地址法;
再哈希法;
链地址法;
建立公共溢出区;
hash总结
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。 复杂度分析: 单纯论查找复杂度:对于无冲突的Hash表而言,查找复杂度为O(1)(注意,在查找之前我们需要构建相应的Hash表)。
使用Hash,我们付出了什么?
我们在实际编程中存储一个大规模的数据,最先想到的存储结构可能就是map,也就是我们常说的KVpair; python 中的map本质就是Hash表,那我们在获取了超高查找效率的基础上,我们付出了什么?
Hash是一种典型以空间换时间的算法,比如原来一个长度为100的数组,对其查找,只需要遍历且匹配相应记录即可,从空间复杂度上来看,假如数组存储的是byte类型数据,那么该数组占用100byte空间。现在我们采用Hash算法,我们前面说的Hash必须有一个规则,约束键与存储位置的关系,那么就需要一个固定长度的hash表,此时,仍然是100byte的数组,假设我们需要的100byte用来记录键与位置的关系,那么总的空间为200byte,而且用于记录规则的表大小会根据规则,大小可能是不定的。
cuipf

